앙페르 회로 법칙

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 앙페르 회로 법칙의 정의 및 형태
3. 직선 전류에 의한 자기장
- 3.1. 도선 외부 (r > R)
- 3.2. 도선 내부 (r < R)
4. 앙페르-맥스웰 방정식 (수정된 앙페르 회로 법칙)
- 4.1. 변위 전류
- 4.2. 앙페르-맥스웰 방정식의 형태
  - 4.2.1. 적분 형태
  - 4.2.2. 미분 형태
5. 앙페르 법칙의 역사와 의의
- 5.1. 앙페르의 법칙 발견
- 5.2. 맥스웰의 수정 및 전자기파 예측
참조

1. 개요

앙페르 회로 법칙은 전류와 자기장의 관계를 설명하는 물리 법칙으로, 전류밀도와 자계강도 사이의 관계를 나타낸다. 이 법칙은 폐곡선을 따라 자기장의 선적분 값이 그 곡선을 통과하는 전류에 비례한다는 것을 의미하며, 적분 형태와 미분 형태로 표현될 수 있다. 앙페르 회로 법칙은 맥스웰에 의해 변위 전류 개념이 추가되어 앙페르-맥스웰 방정식으로 확장되었으며, 이는 전자기파의 존재를 예측하는 데 중요한 역할을 했다.

더 읽어볼만한 페이지

맥스웰 방정식 - 가우스 법칙
가우스 법칙은 전기장과 전하 분포의 관계를 나타내는 전자기학의 기본 법칙으로, 폐곡면을 통과하는 전기장의 플럭스는 그 곡면 내부의 알짜 전하량에 비례하며, 맥스웰 방정식의 일부로 고전 전자기학의 기초를 이룬다.
맥스웰 방정식 - 전자기 유도
전자기 유도는 자기장 변화가 도체에 기전력을 유도하는 현상으로, 패러데이의 유도 법칙과 렌츠의 법칙으로 설명되며, 발전기, 변압기 등에 응용되고 로렌츠 힘, 와전류, 전자기파와 관련된다.
사람 이름을 딴 낱말 - 뒤베르제의 법칙
뒤베르제의 법칙은 선거제도와 정당 수 사이의 관계를 설명하는 가설로, 단순 다수 대표제는 양당제를, 결선투표제와 비례대표제는 다당제를 낳는다는 내용을 제시한다.
사람 이름을 딴 낱말 - 옴의 법칙
옴의 법칙은 1827년 게오르크 옴이 발표한, 전압(V)은 전류(I)와 저항(R)의 곱(V=IR)으로 표현되는, 전압, 전류, 저항 간의 관계를 나타내는 기본 법칙이다.
전자기학 - 전력
전력은 전압과 전류의 곱으로 계산되며, 발전소에서 생산되어 송전 및 배전을 통해 소비자에게 공급되고, 에너지 저장 기술을 통해 안정적으로 공급될 수 있으며, 산업, 상업, 가정 등 다양한 분야에서 소비된다.
전자기학 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.

앙페르 회로 법칙
개요
정의	전류가 폐쇄 루프를 따라 흐를 때, 루프를 통과하는 자기장의 선적분은 루프 내부의 전류의 투과율 상수 곱과 같음
적분 형태
공식	∮C B ⋅ dl = μ0Ienc
설명	∮C는 폐쇄 루프 C에 대한 선적분 B는 자기장 dl은 루프 C의 무한소 길이 요소 μ0는 진공의 투자율 Ienc는 루프 C에 의해 둘러싸인 총 전류
미분 형태 (맥스웰-앙페르 법칙)
공식	∇ × B = μ0J + μ0ε0∂E/∂t
설명	∇ × B는 자기장의 회전 J는 전류 밀도 ε0는 진공의 유전율 ∂E/∂t는 시간에 따른 전기장의 변화율 (변위 전류)
역사적 맥락
앙페르의 원래 법칙	시간에 따라 변하지 않는 전류에 대한 자기장 관계만을 다룸
맥스웰의 수정	변위 전류 항(μ0ε0∂E/∂t)을 추가하여 시간에 따라 변하는 전기장과 자기장을 설명
응용
자기장 계산	대칭적인 전류 분포를 갖는 경우 자기장을 쉽게 계산 가능
예시	무한히 긴 직선 도선 무한 평면 전류 시트 솔레노이드 토로이드
주의 사항
대칭성 요구	앙페르 법칙을 쉽게 적용하기 위해서는 전류 분포에 충분한 대칭성이 있어야 함
변위 전류 고려	시간에 따라 변하는 전기장이 존재하는 경우 변위 전류를 반드시 고려해야 함
관련 개념
관련 법칙	가우스 법칙 자기장에 대한 가우스 법칙 패러데이 유도 법칙 맥스웰 방정식

2. 앙페르 회로 법칙의 정의 및 형태

앙페르 회로 법칙은 전류밀도와 그 전류밀도가 만들어내는 자계강도 사이의 관계를 나타내는 법칙이다. 이 법칙은 적분 형태와 미분 형태, 두 가지로 표현될 수 있다.

적분 형태는 다음과 같다.

: $\oint_C \mathbf{H} \cdot d\mathbf{l} = \int_S \mathbf{J} \cdot d \mathbf{a}$

여기서,

$\mathbf{H}$ 는 자계강도(A/m)
$d\mathbf{l}$ 는 폐곡선 C의 미소 요소
$\mathbf{J}$ 는 폐곡선 C로 둘러싸인 면 S를 통과하는 전류밀도(A/m²)
$\oint_C$ 는 폐곡선 C를 따른 선적분

미분 형태는 다음과 같다.

:

\nabla \times \mathbf{H} =   \mathbf{J}

자계강도 '''H'''는 자속밀도 '''B'''(테슬라)와 진공에서 다음과 같은 관계를 가진다.

:

\mathbf{B} \ = \ \mu_0 \mathbf{H}

여기서

\mu_0

는 투자율(H/m)이며,

\mu_0  = 4 \pi \times 10^{-7}

이다.

앙페르 회로 법칙은 켈빈-스토크스 정리를 통해 적분 형태와 미분 형태가 서로 동등함을 보일 수 있다.

2. 1. 적분 형태

앙페르 회로 법칙의 적분 형태는 임의의 닫힌 곡선 C를 따라 자기장의 선적분을 나타낸다. 곡선 C는 전류가 통과하는 곡면 S (임의적이지만 닫히지 않음—S에 의해 3차원 부피가 둘러싸이지 않음)를 경계짓고 전류를 둘러싼다.^[10]^[11] 이 법칙의 수학적 표현은 어떤 경로(선적분)를 따라 자기장의 순환과 그 둘러싸인 경로(면적분)를 통과하는 전류 간의 관계이다.

전류(자유 전류와 결합 전류의 합)의 관점에서, 닫힌 곡선 C를 따라 자기장 B(단위: 테슬라)의 선적분은 곡면 S(C에 의해 둘러싸임)를 통과하는 총 전류 I_enc에 비례한다. 자유 전류의 관점에서, 닫힌 곡선 C를 따라 자기장 H(단위: A/m)의 선적분은 곡면 S를 통과하는 자유 전류 I_f,enc와 같다.

SI 단위로 표현된 앙페르 회로 법칙의 형태
scope="col" style="width: 15em;" \|	적분 형태	미분 형태
B-장과 총 전류 사용	$\oint_C \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} = \mu_0 \iint_S \mathbf{J} \cdot \mathrm{d}\mathbf{S} = \mu_0I_\mathrm{enc}$	$\mathbf{\nabla} \times \mathbf{B} = \mu_0 \mathbf{J}$
H-장과 자유 전류 사용	$\oint_C \mathbf{H} \cdot \mathrm{d}\boldsymbol{l} = \iint_S \mathbf{J}_\mathrm{f}\cdot \mathrm{d}\mathbf{S} = I_\mathrm{f,enc}$	$\mathbf{\nabla} \times \mathbf{H} = \mathbf{J}_\mathrm{f}$

J는 총 전류밀도(단위: A/m²)
J_f는 자유 전류밀도
∮_C는 닫힌 곡선 C를 따라 닫힌 선적분
∬_S는 곡선 C에 의해 경계 지워진 곡면 S에 대한 면적분
·는 벡터 내적
dl는 곡선 C의 미소 요소(미소 선 요소의 길이와 같은 크기와 곡선 C의 접선에 의해 주어지는 방향을 갖는 벡터)
dS는 곡면 S의 미소 요소의 벡터 면적(즉, 미소 면 요소의 면적과 같은 크기와 곡면 S에 수직인 방향을 갖는 벡터. 법선의 방향은 오른손 법칙에 따라 C의 방향과 일치해야 함)
∇ ×는 회전 연산자.

일반적으로 알려진 앙페르 법칙은 다음과 같다. 닫힌 경로를 따라 자기장의 세기를 더하면, 그 결과는 닫힌 경로를 관통하는 전류의 합에 비례한다. 자기장의 합은 선적분을 사용하여 계산한다.

앙페르는 실험을 통해 두 전류 사이에 작용하는 힘을 관측하고, 그 결과를 앙페르 법칙으로 정리하여 전자기 현상을 설명하는 데 성공했다.

앙페르는 전류가 흐르면 전류의 방향을 오른나사의 진행 방향으로 하였을 때, 오른나사가 회전하는 방향으로 자기장이 발생하는 것을 발견했다. 그림 1처럼 오른손의 엄지를 세우고 손을 쥐면, 전류의 방향을 엄지의 방향으로 했을 때 나머지 손가락의 방향이 자기장의 방향과 일치하기 때문에 '''오른손 법칙'''이라고 불린다. 일본에서는 '''오른나사 법칙'''이라고 부르는 경우가 많다.

예를 들어, 무한히 긴 직선 도선에 전류를 흘린다고 하자. 이때 전류 주위에는 동심원 상에서 오른나사 방향의 자기장이 발생한다. 닫힌 경로로 반지름

r

의 동심원을 취하면 그 위에서 자기장의 세기는 같고, 이것을

H

라고 하자.

앙페르 법칙에 따르면,

:

H = \frac{I}{2 \pi r}

라는 관계가 성립한다. 단,

I

는 전류,

r

은 전류와의 거리이다.

이는 비오-사바르 법칙을 적분한 것과 일치한다.

앙페르의 법칙을 선적분·면적분을 이용하여 일반식으로 나타내면 다음과 같다.

:

\oint_C \boldsymbol{H} \cdot \mathrm{d}\boldsymbol{l} = \int_S \boldsymbol{j} \cdot \mathrm{d}\boldsymbol{S} = I

여기서,

$C$	폐곡선
$S$	C를 경계로 하는 곡면
$\boldsymbol{H}$	자기장의 세기
$\boldsymbol{j}$	전류밀도
$I$	곡면 S를 수직으로 관통하는 총전류
$\mathrm{d}\boldsymbol{l}$	선소벡터
$\mathrm{d}\boldsymbol{S}$	면소벡터

이다.

이 식은 전류에 의해 자기장이 발생한다는 것을 나타낸다.

또한,

: $\oint_C \mathbf{H} \cdot d\mathbf{l} = \int_S \mathbf{J} \cdot d \mathbf{a}$

이며, 각 기호의 의미는 다음과 같다.

$\mathbf{H}$ : 자계강도( A/m )
$d\mathbf{l}$ : 곡선 C의 미소미분요소
$\mathbf{J}$ : 곡선 C가 만드는 표면 S를 통과하는 전류밀도 ( A/m²)
$\mu_0 = 4 \pi \times 10^{-7}$ : 자유공간에서의 투자율 (헨리/m)
$\oint_C$ : 폐곡선 $C$ 위에서의 적분

2. 2. 미분 형태

앙페르 회로 법칙의 미분 형태는 다음과 같이 표현된다.^[10]^[11]

:

\nabla \times \mathbf{H} =   \mathbf{J}

여기서,

$\nabla \times \mathbf{H}$ 는 자계 강도 '''H'''의 회전(curl)을 나타낸다.
'''J'''는 곡선 C가 만드는 표면 S를 통과하는 전류밀도를 나타내며, 단위는 암페어 매 제곱미터(A/m²)이다.

자계 강도 '''H'''는 자속 밀도 '''B''' (단위: 테슬라)와 진공에서 다음과 같은 관계를 가진다.

:

\mathbf{B} \ = \ \mu_0 \mathbf{H}

여기서

\mu_0

는 자기 상수를 나타낸다.

앙페르 회로 법칙은 켈빈-스토크스 정리에 의해 적분 형태와 미분 형태가 서로 동등하다. 또한, SI 단위와 cgs 단위 등 다양한 단위계를 사용하여 표현할 수 있다.

다음은 SI 단위로 표현된 앙페르 회로 법칙의 미분 형태이다.

SI 단위로 표현된 앙페르 회로 법칙의 미분 형태
scope="col" style="width: 15em;" \|	미분 형태
B-장과 총 전류 사용	$\mathbf{\nabla} \times \mathbf{B} = \mu_0 \mathbf{J}$
H-장과 자유 전류 사용	$\mathbf{\nabla} \times \mathbf{H} = \mathbf{J}_\mathrm{f}$

'''J'''는 총 전류밀도(단위: A·m⁻²)
'''J'''_f는 자유 전류밀도

회전(rot)을 이용한 앙페르 법칙의 표현은 다음과 같다.

:

\operatorname{rot} \boldsymbol{H} = \boldsymbol{j}

이 식은 전류에 의해 자기장이 발생한다는 것을 나타낸다.

2. 3. 자기장과 자속 밀도의 관계

자계강도 '''H'''는 자속밀도 '''B'''(테슬라)와 진공에서 다음과 같은 관계를 가진다.

:

\mathbf{B} \ = \ \mu_0 \mathbf{H}

3. 직선 전류에 의한 자기장

앙페르 회로 법칙에 따르면, 무한히 긴 직선 도선에 전류가 흐르면 전류 주위에 동심원 모양의 자기장이 발생한다. 이 자기장의 방향은 오른손 법칙(오른나사 회전 방향)과 같다. 일본에서는 오른나사 법칙이라고 부르기도 한다.

비오-사바르 법칙을 적분하면 앙페르 법칙과 동일한 결과를 얻을 수 있다. 즉, 반지름 $r$ 인 동심원 위에서 자기장의 세기 $H$ 는 다음과 같다.

: $H = \frac{I}{2 \pi r}$

여기서 $I$ 는 전류, $r$ 은 전류와의 거리이다.

3. 1. 도선 외부 (r > R)

도선 외부(r > R)의 경우 자기장의 세기는 그림 1과 같이 원1을 폐경로로 하여 적분한다.

대칭성으로부터 B는 원 위의 모든 점에서 크기가 일정하고 ds에 평행하다.

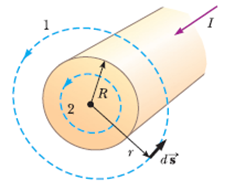
폐경로에 의해 둘러싸인 임의의 면을 통과하는 전체 정상 전류는

I

이므로 앙페르 회로 법칙에 의해

\oint B\centerdot ds = B\oint ds = B(2\pi r) = \mu I

\therefore B = \frac{\mu I}{2\pi r}

3. 2. 도선 내부 (r < R)

도선 내부의 경우 자기장의 세기는 그림 1과 같이 원2를 폐경로로 하여 적분을 한다.

대칭성으로부터 B는 원 위의 모든 점에서 크기가 일정하고 ds에 평행하다.

폐 경로에 의해 둘러싸인 임의의 면을 통과하는 전체 정상 전류

\grave{I}

는 전체 전류

I

보다 작다.

전체 전류에 대한

\grave{I}

의 비율을 구하면

\frac{\grave{I}}{I} = \frac{\pi r^2}{\pi R^2}

이다.

\oint B\centerdot ds = B\oint ds = B(2\pi r) = \mu \grave{I}=\mu\frac{r^2}{R^2} I

\therefore B=(\frac{\mu I}{2\pi R^2})r

4. 앙페르-맥스웰 방정식 (수정된 앙페르 회로 법칙)

제임스 클러크 맥스웰은 축전기에 앙페르 회로 법칙을 적용했을 때 나타나는 문제점을 해결하기 위해 변위전류 개념을 도입하고, 이를 통해 앙페르 회로 법칙을 수정하여 맥스웰 방정식의 일부로 만들었다. 수정된 법칙은 앙페르-맥스웰 방정식으로 불린다.

앙페르-맥스웰 방정식은 적분 형태와 미분 형태로 나타낼 수 있다.

적분 형태:

:

\oint_C \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} =  \iint_S \left( \mu_0 \mathbf{J}+ \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}\right) \cdot \mathrm{d} \mathbf{S}

미분 형태:

:

\mathbf{\nabla}\times \mathbf{B} = \mu_0\mathbf{J}+\mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}

두 식에서

\mathbf{J}

는 자유 전류와 속박 전류를 모두 포함하는 전류 밀도이고,

\varepsilon_0 \frac {\partial \mathbf{E}}{\partial t}

항은 변위 전류를 나타낸다.

맥스웰은 변위전류를 통해 빛이 전자기파의 한 형태임을 예측할 수 있었다.^[12]^[13]^[14]^[15]^[16]

4. 1. 변위 전류

제임스 클러크 맥스웰은 축전기에 앙페르 법칙을 적용할 때 생기는 모순을 보고 이 법칙이 불완전하다고 생각했다.^[12]^[13]^[14]^[15]^[16] 이 문제를 해결하기 위해 그는 변위전류 개념을 만들었고, 이를 통해 맥스웰 방정식에 포함된 일반화된 앙페르 회로 법칙을 만들었다.

맥스웰이 수정한 앙페르 회로 법칙의 적분 형태는 다음과 같다.

:

\oint_C \mathbf{H} \cdot d\mathbf{l} = \int_S \mathbf{J} \cdot d \mathbf{A} +{d \over dt} \int_S \mathbf{D} \cdot d \mathbf{A}

변위전류밀도 '''D'''는 다음과 같다. (단위: 쿨롱/미터²) (진공인 경우)

:

\mathbf{D} \ = \ \varepsilon_0 \mathbf{E}

이 '''앙페르-맥스웰 법칙'''은 다음과 같은 미분 형태로도 나타낼 수 있다.

::

\nabla \times \mathbf{H} =   \mathbf{J} +     \frac{\partial \mathbf{D}}{\partial t}

여기서 두 번째 항이 변위전류에서 나온 것이다.

변위전류 개념을 통해 맥스웰은 빛이 전자기파의 일종임을 정확히 추론할 수 있었다.

앙페르 회로 법칙에는 전하의 연속 방정식과 관련된 문제와 전자기파 전파와 관련된 두 가지 중요한 문제가 있다.

전하의 연속 방정식 관련 문제: 벡터 미적분에서 회전의 발산에 대한 항등식은 벡터장의 회전의 발산이 항상 0이어야 함을 나타낸다. 따라서 원래의 앙페르 회로 법칙은 전류 밀도가 솔레노이드임을 의미하는 $\nabla\cdot \mathbf{J} = 0\,$ 를 나타낸다. 그러나 현실은 시간에 따라 변하는 전하 밀도에 대해 0이 아닌 전하에 대한 연속 방정식 $\nabla\cdot \mathbf{J} = -\frac{\partial \rho}{\partial t} \,$ 을 따른다. 예를 들어, 시간에 따라 변하는 전하 밀도가 판에 존재하는 축전기 회로에서 이러한 현상이 발생한다.
전자기파 전파 관련 문제: 자유 공간에서 회로 법칙은 자기장이 비회전임을 의미하는 $\nabla\times\mathbf{B} = \mathbf{0}\,,$ 를 나타낸다. 그러나 전하에 대한 연속 방정식과의 일관성을 유지하려면 $\nabla\times\mathbf{B} = \frac{1}{c^2}\frac{\partial\mathbf{E}}{\partial t}\,$ 를 만족해야 한다.

이러한 상황을 해결하기 위해 변위 전류를 회로 법칙의 전류 항에 추가해야 한다.

맥스웰은 변위 전류를 유전체 소용돌이 바다의 분극 전류로 생각하여 자기장을 유체역학적 및 기계적으로 모델링했다.^[17] 그는 1861년 논문 "On Physical Lines of Force"의 식 112에 이 변위 전류를 앙페르 회로 법칙에 추가했다.^[18]

진공에서 변위 전류는 전기장의 시간에 따른 변화율과 관련이 있다. 유전체 내부에서도 이러한 변위 전류가 존재하지만, 주요 기여는 유전체 물질의 개별 분자의 분극과 관련이 있다. 전하는 유전체 내에서 자유롭게 흐를 수 없지만, 분자 내의 전하는 전기장의 영향으로 약간 이동할 수 있다. 분자 내의 양전하와 음전하는 인가된 전기장 하에서 분리되어 분극 밀도 '''P'''로 표현되는 분극 상태의 증가를 야기한다. 분극 상태의 변화는 전류와 같다.

변위 전류는 다음과 같이 정의되어 두 가지 기여를 결합한다.^[12]

:

\mathbf{J}_\mathrm{D} = \frac {\partial}{\partial t} \mathbf{D} (\mathbf{r}, \, t) \, ,

여기서 전기 변위장은 다음과 같이 정의된다.

:

\mathbf{D} = \varepsilon_0 \mathbf{E} + \mathbf{P} = \varepsilon_0 \varepsilon_\mathrm{r} \mathbf{E} \, ,

여기서 ε₀는 진공 유전율, ε_r는 상대 유전율, '''P'''는 분극 밀도이다. 변위 전류에 대한 식에서 '''D'''에 대한 이 형태를 대입하면 다음과 같은 두 가지 성분을 갖는다.

:

\mathbf{J}_\mathrm{D} = \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t} + \frac{\partial \mathbf{P}}{\partial t}\,.

오른쪽의 첫 번째 항은 진공에서도 존재한다. 이것은 실제 전하의 이동을 포함하지 않지만, 실제 전류인 것처럼 관련된 자기장을 갖는다. 일부 저자는 이 기여에만 '변위 전류'라는 이름을 적용한다.^[19]

오른쪽의 두 번째 항은 맥스웰이 처음 생각했던 변위 전류로, 유전체 물질의 개별 분자의 분극과 관련이 있다.

맥스웰의 변위 전류에 대한 원래 설명은 유전 매질에서 발생하는 상황에 초점을 맞추었다. 현대에는 이 개념이 물질 매질이 없는 상황, 예를 들어 충전 중인 진공 축전기의 판 사이의 진공에 적용되도록 확장되었다. 변위 전류는 자유 전류가 흐르지 않는 영역에서 자기장을 정확하게 예측하고, 전자기장의 파동 전파를 예측하며, 전하 밀도가 시간에 따라 변하는 경우 전하 보존을 만족시키는 등 전자기 이론의 몇 가지 요구 사항을 충족하기 때문에 오늘날 정당화된다.

4. 2. 앙페르-맥스웰 방정식의 형태

제임스 클러크 맥스웰은 축전기에 앙페르 회로 법칙을 적용했을 때 발생하는 모순을 통해 이 법칙이 완전하지 않다는 것을 발견했다.^[12]^[13]^[14]^[15]^[16] 맥스웰은 이 문제를 해결하기 위해 변위전류 개념을 도입하여 앙페르 회로 법칙을 일반화했고, 이는 맥스웰 방정식에 통합되었다.

일반화된 앙페르 회로 법칙, 즉 앙페르-맥스웰 방정식은 적분 형태와 미분 형태로 표현된다. 두 형태 모두에서 전류 밀도 J는 전도 및 분극 전류 밀도뿐만 아니라 자화 전류 밀도^[21]도 포함한다. 즉, 맥스웰-앙페르 방정식의 우변에 있는 전류 밀도는 다음과 같다.

:

\mathbf{J}_\mathrm{f}+\mathbf{J}_\mathrm{D} +\mathbf{J}_\mathrm{M} = \mathbf{J}_\mathrm{f}+\mathbf{J}_\mathrm{P} +\mathbf{J}_\mathrm{M} + \varepsilon_0 \frac {\partial \mathbf{E}}{\partial t} = \mathbf{J}+ \varepsilon_0 \frac {\partial \mathbf{E}}{\partial t} \, ,

여기서 J_D는 ''변위 전류''이고, J는 자유 전하와 결합 전하의 움직임으로 인한 전류 밀도 기여이다. ∇ ⋅ D = ''ρ''이기 때문에 앙페르의 원래 공식의 전하 연속성 문제는 더 이상 문제가 되지 않으며,^[22] ''ε''₀∂E/∂''t'' 항 때문에 자유 공간에서 파동 전파가 가능해졌다.

맥스웰은 변위 전류를 유전체 소용돌이 바다의 분극 전류로 간주하여 자기장을 유체역학적 및 기계적으로 모델링했다.^[17] 그는 1861년 논문 "On Physical Lines of Force"의 식 112에 이 변위 전류를 앙페르 회로 법칙에 추가했다.^[18]

변위전류 개념을 통해 맥스웰은 빛이 전자기파의 일종임을 정확히 예측할 수 있었다.

4. 2. 1. 적분 형태

제임스 클러크 맥스웰은 축전기에 앙페르 법칙을 적용할 때 생기는 모순을 보고 이 법칙이 불완전하다고 생각했다.^[12]^[13]^[14]^[15]^[16] 이 문제를 해결하기 위해 그는 변위전류 개념을 만들었고, 이를 통해 맥스웰 방정식에 포함된 일반화된 앙페르 회로 법칙을 만들었다.

맥스웰이 수정한 앙페르 회로 법칙의 적분 형태는 다음과 같다.

:

\oint_C \mathbf{H} \cdot d\mathbf{l} = \int_S \mathbf{J} \cdot d \mathbf{A} + {d \over dt} \int_S \mathbf{D} \cdot d \mathbf{A}

변위전류밀도 '''D'''는 다음과 같다. (단위: 쿨롱/미터²)(진공인 경우)

:

\mathbf{D} \ = \ \varepsilon_0 \mathbf{E}

이 '''앙페르-맥스웰 법칙'''은 다음과 같은 미분형으로도 표현된다.

::

\nabla \times \mathbf{H} =   \mathbf{J} +     \frac{\partial \mathbf{D}}{\partial t}

두 번째 항이 변위전류에서 나온 것을 알 수 있다.

변위전류 개념을 통해 맥스웰은 빛이 전자기파의 한 종류라고 정확히 예측할 수 있었다.

자유 전하를 결합 전하와 별도로 처리하면, 맥스웰의 수정을 포함하는 방정식은 '''H'''장에 대한 다음과 같다( '''H'''장은 자화 전류를 포함하기 때문에 '''J'''_M이 명시적으로 나타나지 않는다. '''H'''장 및 참고 참조).^[20]

:

\oint_C \mathbf{H} \cdot \mathrm{d} \boldsymbol{l} =  \iint_S \left( \mathbf{J}_\mathrm{f} + \frac{\partial \mathbf{D}}{\partial t} \right) \cdot \mathrm{d} \mathbf{S}

(적분 형태), 여기서 '''H'''는 자기장(보조 자기장, 자기장 세기 또는 단순히 자기장이라고도 함), '''D'''는 전기 변위장, '''J'''_f는 둘러싸인 전도 전류 또는 자유 전류 밀도이다.

반면, 모든 전하를 동일하게 취급(결합 전하인지 자유 전하인지 여부 무시)하면, 일반화된 앙페르 방정식, 즉 맥스웰-앙페르 방정식은 적분 형태로 다음과 같다.

:

\oint_C \mathbf{B} \cdot \mathrm{d}\boldsymbol{l} =  \iint_S \left( \mu_0 \mathbf{J}+ \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}\right) \cdot \mathrm{d} \mathbf{S}

4. 2. 2. 미분 형태

제임스 클러크 맥스웰은 축전기에 앙페르 법칙을 적용할 때의 모순을 발견하고, 이 법칙이 불완전하다고 결론내렸다. 이 문제를 해결하기 위해 그는 변위전류 개념을 고안하여 맥스웰 방정식에 편입된 일반화된 앙페르 회로 법칙을 만들었다. 앙페르-맥스웰 법칙의 미분 형태는 다음과 같다.^[12]^[13]^[14]^[15]^[16]

::

\nabla \times \mathbf{H} =   \mathbf{J} +     \frac{\partial \mathbf{D}}{\partial t}

여기서 두 번째 항은 변위전류에서 나온 것이다.

맥스웰은 변위전류 개념을 통해 빛이 전자기파의 일종임을 (정확히) 가정할 수 있었다. 앙페르 회로 법칙에는 두 가지 중요한 문제가 있는데, 첫째는 전하의 연속 방정식과 관련된 문제이다. 벡터 미적분에서 회전의 발산에 대한 항등식은 벡터장의 회전의 발산이 항상 0이어야 함을 나타내므로, 원래의 앙페르 회로 법칙은 전류 밀도가 솔레노이드임을 의미한다. 그러나 현실은 전하에 대한 연속 방정식을 따르며, 이는 시간에 따라 변하는 전하 밀도에 대해 0이 아니다. 예를 들어, 시간에 따라 변하는 전하 밀도가 판에 존재하는 축전기 회로에서 발생한다.

둘째, 전자기파의 전파와 관련된 문제가 있다. 예를 들어, 자유 공간에서 회로 법칙은 자기장이 비회전임을 의미하지만, 전하에 대한 연속 방정식과의 일관성을 유지하려면 변위 전류의 기여를 회로 법칙의 전류 항에 추가해야 한다.

맥스웰은 변위 전류를 유전체 소용돌이 바다의 분극 전류로 생각하여 자기장을 유체역학적 및 기계적으로 모델링했다.^[17] 그는 1861년 논문 "On Physical Lines of Force"의 식 112에 이 변위 전류를 앙페르 회로 법칙에 추가했다.^[18]

자유 전하를 결합 전하와 별도로 처리하면, 맥스웰의 수정을 포함하는 방정식은 자기장()에 대한 미분 형태는 다음과 같다.

:

\mathbf{\nabla} \times \mathbf{H} = \mathbf{J}_\mathrm{f}+\frac{\partial \mathbf{D}}{\partial t} \, .

여기서 는 보조 자기장, 자기장 세기 또는 단순히 자기장이라고도 하며, 는 전기 변위장, 는 둘러싸인 전도 전류 또는 자유 전류 밀도이다.

반면, 모든 전하를 동일하게 취급하면, 일반화된 앙페르 방정식, 즉 맥스웰-앙페르 방정식은 미분 형태로 다음과 같다.

::

\mathbf{\nabla}\times \mathbf{B} = \mu_0\mathbf{J}+\mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}

두 형태 모두 는 자화 전류 밀도^[21]뿐만 아니라 전도 및 분극 전류 밀도를 포함한다. 이기 때문에 앙페르의 원래 공식의 전하 연속성 문제는 더 이상 문제가 되지 않으며,^[22] 항 때문에 이제 자유 공간에서 파동 전파가 가능해졌다.

변위 전류를 추가함으로써 맥스웰은 빛이 전자기파의 한 형태라는 가설을 세울 수 있었다.

5. 앙페르 법칙의 역사와 의의

한스 크리스티안 외르스테드가 1820년 전류와 자기장의 관계를 발견한 후, 앙드레 마리 앙페르는 전류가 흐르는 두 도선 사이의 자기력을 연구하여 앙페르의 힘 법칙을 발견했다. 1850년대 제임스 클러크 맥스웰은 이 결과들과 다른 실험 결과들을 "On Faraday's Lines of Force"라는 논문에서 하나의 법칙으로 통합했다.^[9] 이 법칙은 주어진 전류와 관련된 자기장을 결정하거나, 주어진 자기장과 관련된 전류를 결정한다.

원래의 앙페르 회로 법칙은 닫힌 회로에서 흐르는 연속적인 정상 전류에 대한 정자기학적 상황에만 적용되었다. 그러나 시간에 따라 변하는 전기장을 가진 시스템의 경우, 원래 법칙은 맥스웰의 수정 항을 포함하도록 수정되어야 한다. 일반적으로 알려진 앙페르 법칙은 닫힌 경로를 따라 자기장의 세기를 더하면, 그 결과가 닫힌 경로를 통과하는 전류의 합에 비례한다는 것이다. 이 자기장의 합은 선적분을 사용하여 계산한다.

5. 1. 앙페르의 법칙 발견

한스 크리스티안 외르스테드(Hans Christian Ørsted)는 1820년 전류가 흐르는 도선 근처의 나침반 바늘이 움직이는 것을 보고 전류가 자기장을 만든다는 것을 발견했다.^[6]^[7] 그는 직선 도선 주변의 자기장을 연구하여 다음과 같은 사실을 알아냈다.^[8]

자기력선의 특징
자기 력선은 전류가 흐르는 도선을 감싼다.
자기 력선은 도선에 수직인 평면에 있다.
전류 방향이 반대가 되면 자기장 방향도 반대가 된다.
자기장 세기는 전류 세기에 정비례한다.
자기장 세기는 도선과의 거리에 반비례한다.

이 발견은 전기와 자기의 관계에 대한 많은 연구를 이끌었다. 앙드레 마리 앙페르(André-Marie Ampère)는 전류가 흐르는 두 도선 사이의 자기력을 연구하여 앙페르의 힘 법칙을 발견했다. 1850년대 제임스 클러크 맥스웰(James Clerk Maxwell)은 이 결과들을 "On Faraday's Lines of Force"에서 하나의 법칙으로 정리했다.^[9]

앙페르는 실험을 통해 두 전류 사이에 힘이 작용하는 것을 관찰하고, 이 결과를 앙페르 법칙으로 정리하여 전자기 현상을 설명했다.

앙페르는 전류가 흐르면 전류 방향을 오른나사의 진행 방향으로 할 때, 오른나사가 회전하는 방향으로 자기장이 생기는 것을 발견했다. 그림 1처럼 오른손 엄지를 세우고 손을 쥐면, 전류 방향을 엄지 방향으로 했을 때 나머지 손가락 방향이 자기장 방향과 일치해서 '''오른손 법칙'''이라고 한다. 일본에서는 '''오른나사 법칙'''이라고도 한다.

예를 들어, 무한히 긴 직선 도선에 전류를 흘리면, 전류 주위에 동심원 모양으로 오른나사 방향의 자기장이 생긴다. 닫힌 경로로 반지름 $r$ 의 동심원을 잡으면 그 위에서 자기장 세기는 같다.

앙페르 법칙에 따르면,

: $H = \frac{I}{2 \pi r}$

의 관계가 나타난다. ( $I$ 는 전류, $r$ 은 전류와의 거리)

이는 비오-사바르 법칙을 적분한 결과와 같다.

5. 2. 맥스웰의 수정 및 전자기파 예측

제임스 클러크 맥스웰은 축전기에 앙페르 법칙을 적용할 때 모순이 생기는 것을 발견하고, 이 법칙이 불완전하다고 결론 내렸다.^[12]^[13]^[14]^[15]^[16] 이 문제를 해결하기 위해 변위전류 개념을 고안하여 맥스웰 방정식에 포함된 일반화된 앙페르 회로 법칙을 만들었다.

맥스웰이 수정한 앙페르 회로 법칙의 적분 형태는 다음과 같다.

:

\oint_C \mathbf{H} \cdot d\mathbf{l} = \int_S \mathbf{J} \cdot d \mathbf{A} +{d \over dt} \int_S \mathbf{D} \cdot d \mathbf{A}

변위전류밀도 '''D'''는 진공에서 다음과 같다. (단위: 쿨롱/미터²)

:

\mathbf{D} \ = \ \varepsilon_0 \mathbf{E}

이 '''앙페르-맥스웰 법칙'''은 미분 형태로도 표현된다.

::

\nabla \times \mathbf{H} =   \mathbf{J} +     \frac{\partial \mathbf{D}}{\partial t}

여기서 두 번째 항이 변위전류에서 나온 것이다.

맥스웰은 변위전류 개념을 통해 빛이 전자기파의 일종임을 정확히 예측할 수 있었다. 그는 변위 전류를 유전체 소용돌이 바다의 분극 전류로 생각하여 자기장을 유체역학적 및 기계적으로 모델링했다.^[17] 1861년 논문 "On Physical Lines of Force"의 식 112에 이 변위 전류를 앙페르 회로 법칙에 추가했다.^[18]

원래 앙페르 회로 법칙에는 두 가지 중요한 문제가 있었다. 첫째, 전하의 연속 방정식과 관련된 문제로, 벡터 미적분에서 회전의 발산 항등식에 따라 벡터장의 회전의 발산은 항상 0이어야 한다. 따라서

:

\nabla\cdot(\nabla\times\mathbf{B}) = 0 \,,

이고, 원래의 앙페르 회로 법칙은 다음을 의미한다.

:

\nabla\cdot \mathbf{J} = 0\,,

즉, 전류 밀도가 솔레노이드임을 의미한다. 그러나 현실은 일반적으로 전하에 대한 연속 방정식을 따른다.

:

\nabla\cdot \mathbf{J} = -\frac{\partial \rho}{\partial t} \,,

이는 시간에 따라 변하는 전하 밀도에 대해 0이 아니다. 예를 들어, 시간에 따라 변하는 전하 밀도가 판에 존재하는 축전기 회로에서 발생한다.

둘째, 전자기파의 전파와 관련된 문제가 있었다. 예를 들어,

:

\mathbf{J} = \mathbf{0}\,,

인 자유 공간에서 회로 법칙은 다음을 의미한다.

:

\nabla\times\mathbf{B} = \mathbf{0}\,,

즉, 자기장이 비회전임을 의미하지만, 전하에 대한 연속 방정식과의 일관성을 유지하려면 다음을 만족해야 한다.

:

\nabla\times\mathbf{B} = \frac{1}{c^2}\frac{\partial\mathbf{E}}{\partial t}\,.

이러한 상황을 다루기 위해 변위 전류의 기여를 회로 법칙의 전류 항에 추가해야 했다. 앙페르 법칙은 맥스웰에 의해 확장되고 수학적으로 정비되어 맥스웰 방정식의 네 방정식 중 하나가 되었다(앙페르-맥스웰 방정식).

참조

_[1] 서적 Ampère's electrodynamics: analysis of the meaning and evolution of Ampère's force between current elements, together with a complete translation of his masterpiece: Theory of electrodynamic phenomena, uniquely deduced from experience http://www.ifi.unica[...] Apeiron 2015
_[2] 웹사이트 On Physical Lines of Force https://archive.org/[...] New York, Dover Publications
_[3] 서적 A Student's Guide to Maxwell's Equations https://books.google[...] Cambridge University Press 2008
_[4] 서적 Classical Electromagnetism in a Nutshell https://books.google[...] Princeton University Press 2012
_[5] 서적 Physics for Scientists and Engineers: Foundations and Connections, Extended Version https://books.google[...] Cengage Learning 2016
_[6] 학술지 Experiments on the effect of a current of electricity on the magnetic needles Baldwin, Craddock, Joy 1820
_[7] 서적 Romanticism and the Sciences https://books.google[...] CUP Archive 1990
_[8] 서적 Basic Electrical Engineering, Vol. 1 https://books.google[...] Tata McGraw-Hill 1986
_[9] 웹사이트 On Faraday's Lines of Force https://archive.org/[...] New York, Dover Publications
_[10] 서적 Magnetic Fields: A comprehensive theoretical treatise for practical use https://books.google[...] Wiley
_[11] 서적 Electromagnetic Theory https://books.google[...] Courier-Dover Publications
_[12] 서적 Classical Electrodynamics https://archive.org/[...] Wiley
_[13] 서적 Introduction to Electrodynamics Pearson/Addison-Wesley
_[14] 서적 Electromagnetic Theory https://books.google[...] Dover Publications
_[15] 서적 Wave Motion https://books.google[...] Cambridge University Press
_[16] 서적 Electromagnetism https://books.google[...] Courier Dover Publications
_[17] 서적 Innovation in Maxwell's Electromagnetic Theory: Molecular Vortices, Displacement Current, and Light https://books.google[...] Cambridge University Press
_[18] 학술지 On Physical Lines of Force http://upload.wikime[...]
_[19] 서적 Introduction to Electrodynamics https://archive.org/[...] Prentice Hall
_[20] 서적 Advanced University Physics https://books.google[...] CRC Press
_[21] 서적 Advanced University Physics https://books.google[...] CRC Press
_[22] 문서 Magnetization current

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com